Sanskrit linguistic resources
Sanskrit MorphologyBackgroundThis documents XML data banks of Sanskrit forms given with their morphological taggings. They are produced mechanically by the declension and conjugation engines of the Sanskrit Heritage Platform, processing the Sanskrit lexicon underlying the Sanskrit Heritage Dictionary. The version used for this generation is available here as a PDF document.
Databanks descriptionWe provide here inflected forms and morphemes derived from the root forms defined in the Sanskrit Heritage Dictionary. These forms are presented as lemmas linking each form to its stem entry by possible morpho-phonetic operations. We limit ourselves to classical Sanskrit, and do not cover precative, subjunctive, injunctive and conditional forms of the verbs. At present, we provide for two transliteration schemas, respectively WX, used by the Department of Sanskrit Studies at University of Hyderabad and SLP1, used by the Sanskrit Library. The WX version is available as a downloadable gzip-compressed XML file WX morphology, conformant to its dtd. The SL version is available as a downloadable gzip-compressed XML file SL morphology, conformant to its dtd.Intellectual PropertyAll these linguistic data banks are Copyrighted Gérard Huet 1994-2025. They are derived from the Sanskrit Heritage Dictionary version 3.70 dated 2025-07-20.Use of these linguistic resources is granted according to the Lesser General Public Licence for Linguistic Resources. A pdf copy of this license is provided here: LGPLLR.pdf. MethodologyWe deal here with a mixture of derivational and inflexional morphology. For instance, from the roots we generate verbal and propositional stems, and from these stems we generate in turn inflected forms: conjugated forms from the verbal stems, and declined forms from the participial stems. But at present we do not generate mechanically primary nominal stems from roots, nor secondary nominal stems from primary ones, because of overgeneration. The nominal stems, as well as the undeclinable forms, are taken from the lexicon, that lists also some frequent participles.This organization entails a different role in our morphological data bases. The basic morphological categories correspond to lexical phases, which are atomic letters in the defining grammar of Sanskrit word. The forms listed in these data bases act as morphemes of this high-level morphological definition, which is recursive, since compounding may be iterated, as well as preverb formation, to a certain extent. But this recursion power is limited, in the sense that the grammar of a word is a regular one (type 0 in the Chomsky hierarchy), and its recognizer is a finite automaton, whose states are precisely the lexical categories indexing the basic data bases. This definition of word implements correctly the geometry of constructions such as absolutives (which fall in two distinct categories, the preverb form and the root form) and periphrastic phrases (periphrastic futures with substantives, and periphratic perfects as prefixes of finite perfect forms of the auxiliary roots as, bhū and kṛ] which are duplicated in a specific auxiliary lexicon). Here is a simplified diagram of the current state space of our lexer. 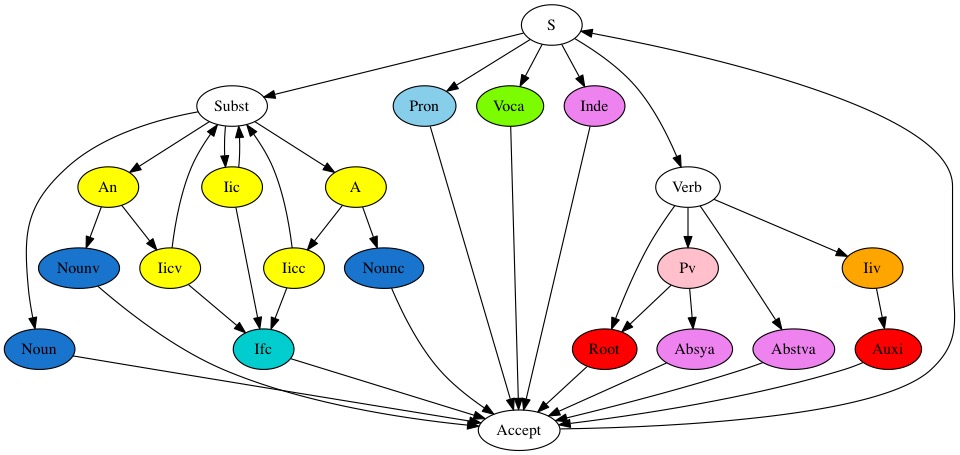
As usual in a non-deterministic search algorithm (here all the possible parsings of a sentence as a sandhied stream of forms), we have two pitfalls, silence and noise. Silence (lack of recall) means incompleteness. Some legal Sanskrit sentences may fail to be recognized. Typicallly, some root word may be missing from the base lexicon, or some Vedic form may use some construction rare in the later language, like precative or subjunctive. Compounding gives rise to two complications, the raising of new cases by bahuvrīhi compounding, and the formation of avyayībhava compounds. Some of these constructions are treated incompletely. The opposite of silence is noise (lack of precision), that is overgeneration. We deal with overgeneration in the syntactico-semantic layer of our tagger, which filters out combinations of tags inconsistent with semantic role assignments. We shall not discuss this technology further in this note on morphology, and refer the interested reader to our Sanskrit reader demonstration page and its Reference manual. We remark that the respective data bases can be interrogated online by our stemmer interface. But note that verbal forms prefixed by preverbs are analysed by the tagger as non-atomic words, and only root forms and their secondary conjugations are recognized by the stemmer. HelpQuestions concerning these resources should be addressed to Gérard Huet. All suggestions for improvements will be gratefully considered. |
